Microsoft Flight Simulator Handbook
by Jonathan M. Stern
Pitot-Static Instruments
The airspeed indicator, vertical speed indicator, and altimeter are components of the pitot-static system (see Figure 2.19).
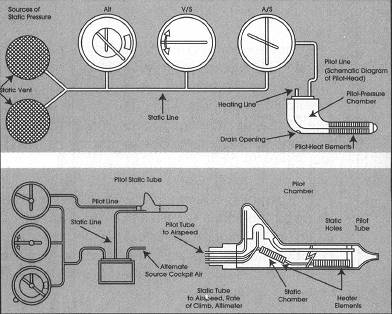
The airspeed indicator is the only instrument connected to the pitot tube. All three instruments, however, are connected to the static source. The airspeed indicator shows the indicated airspeed of the airplane in nautical miles per hour (knots). One nautical mile is equal to 1.15 statute miles or one minute of longitude. Accordingly, one degree of longitude is 60 nautical miles.
Two pilots of identical height, weight, and flying technique buy identical Cessnas, the Model 182RG, on the same day. One pilot keeps his plane in Denver (the Mile High City), the other in Seattle, at Boeing Field. Which one will likely wear out the tires first?
The answer is that the Denver-based pilot will likely be the first to wear out the tires; the reason is density altitude (see Figure 2.20).

Density altitude is the great determinant of aircraft performance. Density altitude, among other things, affects the measurement of airspeed. The acronym ICE T is useful for remembering the various types of airspeed: Indicated, Calibrated, Equivalent, and True. Density altitude and the ICE T acronym help to explain why the Denver pilot will spend more than the West Coast pilot on tires.
Imagine a one-inch by one-inch pipe so tall that it stands from the surface of the Earth and runs up to the top of Earth's atmosphere. On a standard day, the air in the pipe weighs 14.7 pounds.
It is this physical property of the atmosphere that allows you to measure altitude with a barometric altimeter. The altimeter is calibrated in inches of mercury. The 14.7 pounds per square inch equates to 29.92" Hg. In the lower atmosphere, the altitudes at which your Cessna 182RG operates, the pressure lapse rate is approximately 1" Hg per 1,000 feet of altitude.
Accordingly, on a standard day, you expect the pressure at 10,000 feet Mean Sea Level to be approximately 19.92" Hg. As the pressure decreases, the number of molecules in a given volume of air decreases. As a result, the airplane's capability to create lift decreases with altitude. There is also a corresponding decrease in drag, but, at the same time, your normally aspirated (non-turbocharged) engine produces less power, and your propeller becomes less and less able to pull you forward through the air.
The airplane doesn't know whether it's at sea level or at 5,000 feet, It does, however, need the same number of air molecules rolling over its wings in order to generate sufficient lift for takeoff. Because the molecules are fewer and farther between at higher altitudes, the airplane needs to go faster at altitude than it does at sea level to generate sufficient lift for takeoff (see Figure 2.21).

Temperature also has a significant effect on aircraft performance, expanding the air and reducing its density. The higher the temperature, the lower the density of the air. The lower the temperature, the higher the density of the air. Moreover, atmospheric pressure may vary from its standard, which also affects performance.
Pilots have a common reference for correlating the pressure/temperature conditions at a given time to the expected performance of the aircraft. The common reference is density altitude. First start with those conditions that have been labeled standard. A standard day is one on which the pressure at sea level is 29.92" Hg, the temperature at sea level is 59° F/ 15° C, and the pressure and temperature lapse at a rate of 1" Hg/1,000 feet and 3.5° F/2° C per 1,000 feet, respectively (see Figure 2.22).

Density altitude is the altitude which, under standard conditions, yields the same performance. To calculate density altitude, one must first determine the pressure altitude and correct it for nonstandard temperature.
Pressure altitude may be determined by setting the airplane's altimeter to 29.92" and reading the indicated altitude. Alternatively, pressure altitude may be calculated if the altimeter setting is known. If, for example, the airport field elevation is 1,000 feet and the altimeter setting is 30.02" Hg, the pressure altitude is calculated to be 900 feet using the following formula:
Pressure Altitude = MSL Altitude + (1000 * (29.92-Altimeter Setting))
Density altitude may then be computed using a graph or a flight computer (when I learned to fly, these were whiz-wheels; today, there are also electronic calculators). Figure 2.23 is a graph that can be used to determine density altitude from pressure altitude-temperature combinations.
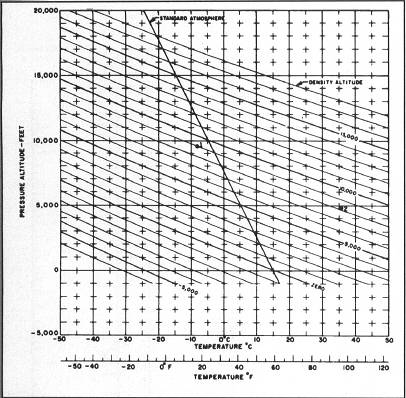
Table of Contents
Previous Section: Instruments
Next Section: Airspeed Indicator
